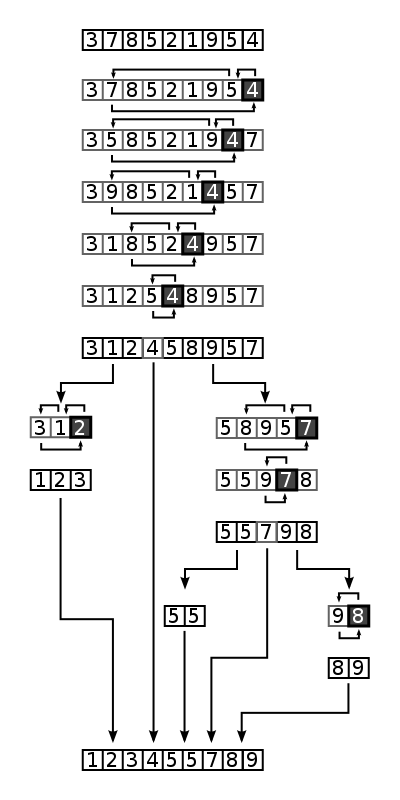
Quicksort is a divide-and-conquer algorithm. It works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively. This can be done in-place, requiring small additional amounts of memory to perform the sorting.

Quicksort is a comparison sort, meaning that it can sort items of any type for which a “less-than” relation (formally, a total order) is defined. Efficient implementations of Quicksort are not a stable sort, meaning that the relative order of equal sort items is not preserved.

Steps

1. it selects a value from the list, which serves as a pivot value to divide the list into two sublists. One sublist contains all the values that are less than the pivot value, while the other sublist contains the values that are greater than or equal to the pivot value. This process is also called partitioning. The strategy of choosing a pivot value can vary. Typically, one can choose the first element in the list as the pivot, or randomly pick an element from the list.
2. After the partitioning process, the original list is then reduced into two smaller sublists. We then recursively sort the two sublists.
3. After the partitioning process, we are sure that all elements in one sublist are less or equal than any element in another sublist. Therefore, we can simply concatenate the two sorted sublists that we obtain in step [2] to obtain the final sorted list.

Base cases in Step2 are either when the input list is empty or the empty list contains only a single element.

Pseudocode

• Lomuto partition scheme

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p - 1)
        quicksort(A, p + 1, hi)

algorithm partition(A, lo, hi) is
    pivot := A[hi]
    i := lo
    for j := lo to hi do
        if A[j] < pivot then
            swap A[i] with A[j]
            i := i + 1
    swap A[i] with A[hi]
    return i

• Hoare partition scheme

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p)
        quicksort(A, p + 1, hi)

algorithm partition(A, lo, hi) is
    pivot := A[⌊(hi + lo) / 2⌋]
    i := lo - 1
    j := hi + 1
    loop forever
        do
            i := i + 1
        while A[i] < pivot
        do
            j := j - 1
        while A[j] > pivot
        if i ≥ j then
            return j
        swap A[i] with A[j]

Time Complexity

• In best case: $O(Nlog_{2}N)$
• In worst case: $O(N^2)$

Reference

• https://en.wikipedia.org/wiki/Quicksort