A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

Coding by C:

#define LSB(i) ((i) & -(i)) // zeroes all the bits except the least significant one
//One based indexing is assumed
int A[SIZE+1];

int sum(int i) // Returns the sum from index 1 to i
{
    int sum = 0;
    while (i > 0)
        sum += A[i], i -= LSB(i);
    return sum;
}

void add(int i, int k) // Adds k to element with index i
{
    while (i <= SIZE)
        A[i] += k, i += LSB(i);
}

Coding By Swift:

var cache = Array(repeating: 0, count: SIZE)
// Add k to element with index x
func update(_ x: Int, _ k: Int) {
	var x = x
	while x < SIZE {
		cache[x] += k
		x += (x & -x)
	}
}

// return sum from index 0 to x
func get(_ x: Int) -> Int {
	var x = x
	var res = 0
	while x > 0 {
		res += cache[x]
		x -= (x & -x)
	}
	return res
}

Background

By straightforward implementation without using bit. Example: an array is [2, 3, -1, 0, 6] the length 3 prefix [2, 3, -1] with sum 2 + 3 + -1 = 4).

2 Operations:

1. point update(i): Change value stored at index i
2. range sum(k): Find sum of a prefix of length k

int a[] = {2, 1, 4, 6, -1, 5, -32, 0, 1};
void update(int i, int v)   //assigns value v to a[i]
{
    a[i] = v;
}
int prefixsum(int k)    //calculate the sum of all a[i] such that 0 <= i < k
{
   int sum = 0;
   for(int i = 0; i < k; i++)
        sum += a[i];
   return sum;
}

This will out of time limit for large dataset. One efficient solution is use segment tree to perform both operation in $O(logN)$ time.

Binary Indexed Tree require less space and are very easy to implement.

Isolate last set bit

Example: number x = 1110(in binary)

So, x & -x gives the last set bit in a number.

Description

$x = a1b$ (in binary) is the number whose last set bit is we want.

$a$ is some binary sequence of any length of 1’s and 0’s, $b$ is some sequence of any length but of 0’s only. The 1 bit between $a$ and $b$ is the last set bit.

Example: $x = 10(in decimal) = 1010(in binary)$, the last set bit is given by $ x\&(-x) = (10)1(0) \& (01)1(0) = 0010 = 2(in decimal) $

Basic Idea of Binary Indexed Tree

For a given array, we can maintain an array $BIT[]$, which at any index we can store sum of some numbers of the given array. This also be called a partial sum tree.

Example: array [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]

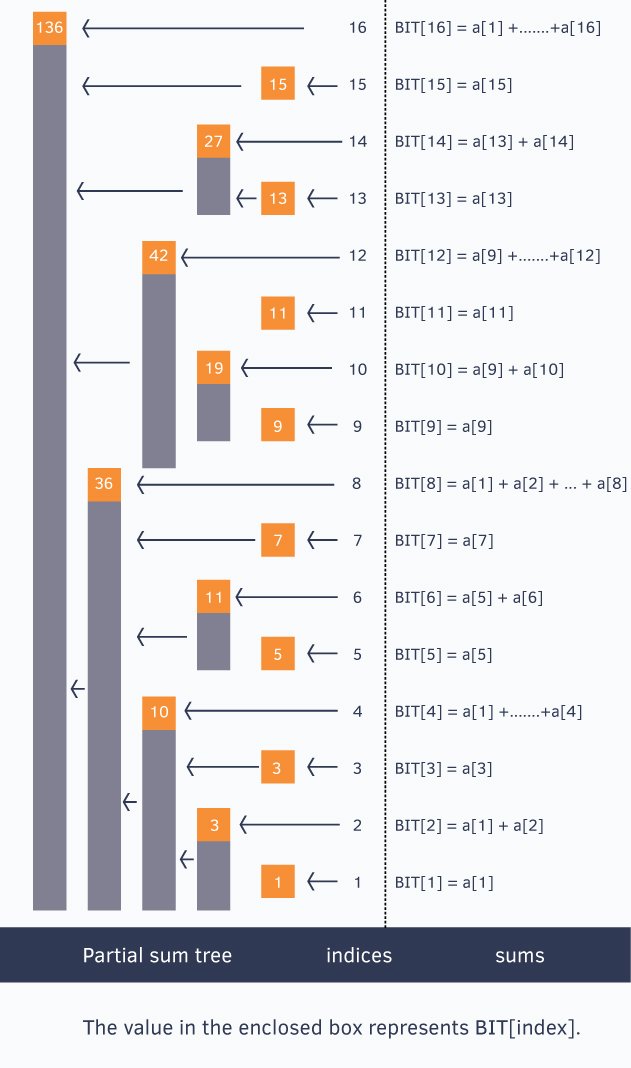
Each enclosed box denotes the value $BIT[index]$, each $BIT[index]$ stores partial sum of some numbers.

Every index $i$ in the $BIT[]$ array stores the cumulative sum from $ i \ to \ i-(1 « r) + 1 $ (both inclusive), where $r$ represents the last set bit in index $i$.

Construct Tree

$BIT[]$ is array of size $1+a[]$, initially is 0. Call $update()$ operation to construct the Binary Indexed Tree

//add "delta" at index "x"
void update(int x, int delta) {
    for(; x <= n; x += x&-x)
          BIT[x] += delta;
}

Example: call $update(13, 2)$, $13, 14, 16$ cover index 13, we need to add 2 to them also.

In this way, $update()$ operation update all indices of $BIT[]$ which cover index $x$ and maintain $BIT[]$. The loop runs at most the number of bits in index $x(<= n)$, so the update operation takes at most $O(log_{2}n)$ time.

Query Prefix Sum

//returns the sum of first x elements in given array a[]
int query(int x) {
     int sum = 0;
     for(; x > 0; x -= x&-x)
         sum += BIT[x];
     return sum;
}

Example: call $query(14)$

The loop iterates at most number of bits in $x$, which will be at most $n$ (the size of given array). So query operation takes $O(log_{2}n)$ time.

When to use

Before going for Binary Indexed tree to perform operations over range, better to confirm:

• Associative. i.e f(f(a, b), c) = f(a, f(b, c)) this is true even for seg-tree
• Has an inverse. eg:
  • addition has inverse subtraction (this example we have discussed)
  • Multiplication has inverse division
  • gcd() has no inverse, so we can’t use BIT to calculate range gcd’s
  • sum of matrices has inverse
  • product of matrices would have inverse if it is given that matrices are degenerate i.e. determinant of any matrix is not equal to 0

• Space Complexity: $O(N)$ where N is array size
• Time Complexity: $O(logN)$ for each operation(update, query)
• Applications:
  • Binary Indexed trees are used to implement the arithmetic coding algorithm.
  • Binary Indexed Tree can be used to count inversions in an arry in $O(N * logN)$ time

Reference

• https://www.hackerearth.com/practice/notes/binary-indexed-tree-or-fenwick-tree/
• https://en.wikipedia.org/wiki/Fenwick_tree