Red Black Tree

Mar 5, 2020

Tree

Algorithm

Red-Black Tree is a binary search tree. It add one more color property at each node, which would be red or black. By using the color, red-black tree can make sure there is no route length larger than 2*other route. Thus it is almost balanced.

The property:

Each node is either red or black
Root node is black
Each child node(NIL) is black
If one node is red, then its 2 children is black
From each node to its successor node, contains same amount of black node(black-height which should at most 2(lg(n+1)))

Operations

For a binary search tree, SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PRECESSOR would take O(logn) time. Red-black tree is also a binary search tree, so in these operations, the time is same. For INSERT & DELETE, we will discuss later how to do it in O(logn) time and also keep the edited one as a red-black tree.

Rotation

In INSERT & DELETE, it will modify the tree, which might not satisfy the above requirements. For keeping the edited one also as a red-black tree, we could rotate the tree.

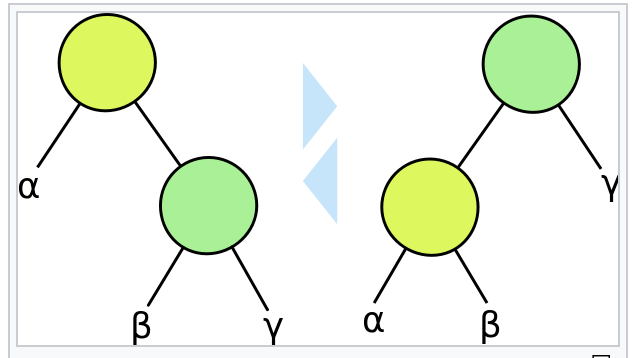
tree_rotation

Pseudocode

// LEFT-ROTATE(T, x)
y = x.right  			// set y
x.right = y.left		// turn y's left subtree into x's right subtree
if y.left != T.nil
	y.left.p = x
y.p = x.p				// link x's parent to y
if x.p == T.nil
	T.root = y
elseif x == x.p.left
	x.p.left = y
else x.p.right == y
y.left = x				// put x on y's left
x.p = y

The left-rotation & right-rotation can be done in O(1) time. In rotation operation, only change the pointer, other properties are keeping previously.

Insert

Insert the node as normal insertion first, then set its color to red, then for keeping the red-black tree property, use RB-INSERT-FIXUP to update the node color & rotate the node.

Pseudocode

// RB-INSERT(T, z)
y = T.nil
x = T.root
while x != T.nil
	y = x
	if z.key < x.key
		x = x.left
	else x = x.right
z.p = y
if y == T.nil
	T.root = z
elseif z.key < y.key
	y.left = z
else y.right = z
z.left = T.nil
z.right = T.nil
z.color = red
RB-INSERT-FIXUP(T,z)

// RB-INSERT-FIXUP(T,z)
while z.p.color == red
	if z.p == z.p.p.left
		y = z.p.p.right
		if y.color == red 		// case 1
			z.p.color = black
			y.color = black
			z.p.p.color = red
			z = z.p.p
		elseif z == z.p.right	// case 2
			z = z.p
			LEFT-ROTATE(T,z)
		z.p.color = black		// case 3
		z.p.p.color = red
		RIGHT-ROTATE(T, z.p.p)
	else same as then clause with right & left exchanged
T.root.color = blcak

Case 1: z.p.p.right is red
Case 2: z.p.p.right is black && z is a right node
Case 3: z.p.p.right is black && z is a left node

Time complexity: since the height of a red-black tree is O(lgn), only at case 1, pointer will move up, so at most O(lgn), otherwise, we will only run while for 2 times.

Delete

Pseudocode

// RB-TRANSPLANT(T, u, v)
if u.p == T.nil
	T.root = v
elseif u == u.p.left
	u.p.left = v
else u.p.right = v
v.p = u.p

// RB-DELETE(T, z)
y = z
yoriginalcolor = y.color
if z.left == T.nil
	x = z.right
	RB-TRANSPLANT(T, z, z.right)
elseif z.right == T.nil
	x = z.left
	RB-TRANSPLANT(T, z, z.left)
else y = TREE-MINIMUM(z.right)
	yoriginalcolor = y.color
	x = y.right
	if y.p == z
		x.p = y
	else RB-TRANSPLANT(T, y, y.right)
		y.right = z.right
		y.right.p = y
	RB-TRANSPLANT(T, z, y)
	y.left = z.left
	y.left.p = y
	y.color = z.color
if yoriginalcolor == black
	RB-DELETE-FIXUP(T, x)

// RB-DELETE-FIXUP(T, x)
while x != T.root && x.color == black
	if x == x.p.left
		w = x.p.right
		if w.color == red									// case 1
			w.color = black
			w.p.color = red
			LEFT-ROTATE(T, x.p)
			w = x.p.right
		if w.left.color == black && w.right.color == black	// case 2
			w.color = red
			x = x.p
		elseif w.right.color == black						// case 3
			w.left.color = black
			w.color = red
			RIGHT-ROTATE(T, w)
			w = x.p.right
		w.color = x.p.color									// case 4
		x.p.color = black
		w.right.color = black
		LEFT-ROTATE(T, x.p)
		x = T.root
	else same s then clause with right and left exchange
x.color = black

case 1: x brother w is red
case 2: x brother w is black && w’s 2 children is black
case 3: x brother w is black, w’s left children is red, w’s right children is black
case 4: x brother w is black, w’s right children is red

Time complexity: case 1,3,4 have constant color changing, and at most rotate 3 times, case 2 is the only case while would be repeat, pointer x will move up at most O(lgn) times. Do at most 3 rotations.

Reference

https://en.wikipedia.org/wiki/Red–black_tree

https://en.wikipedia.org/wiki/Tree_rotation

https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm

Published on 05 Mar 2020 • Find me on Facebook, Twitter!

Comments

Join the discussion for this article at here . Our comments is using Github Issues. All of posted comments will display at this page instantly.