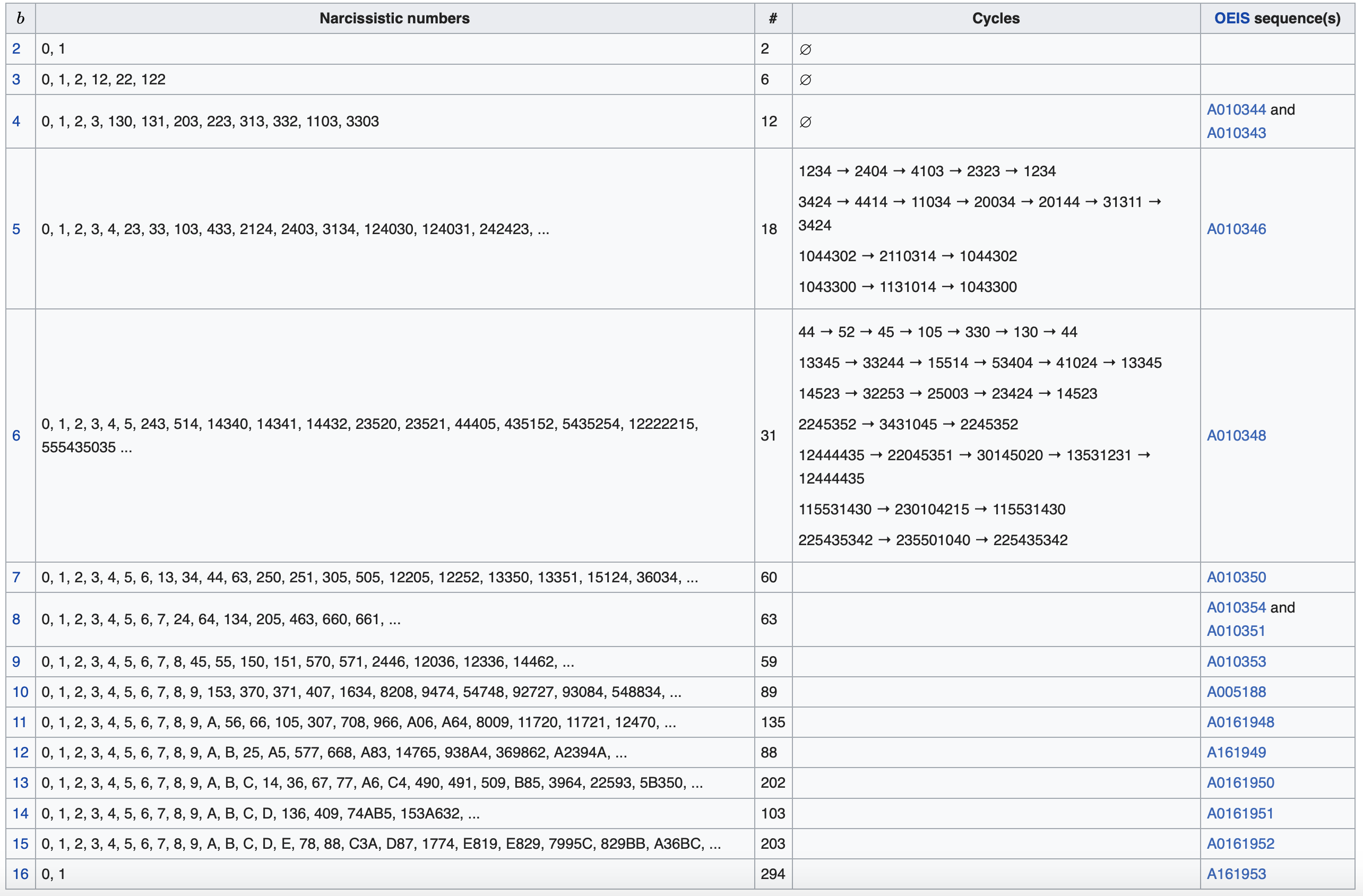
Narcissistic Number

In number theory, a narcissistic number(also known as a pluperfect digital invariant (PPDI), an Armstrong number or a plus perfect number) in a given number base b is a number that is the sum of its own digits each raised to the power of the number of digits.

For base b > 1, \(F_{b}(n)=\sum _{i=0}^{k-1}d_{i}^{k}\) where \(k=\lfloor \log _{b}{n}\rfloor +1\) is the number of digits in the number of digits in the number in base b, and \(d_{i}={\frac {n{\bmod {b^{i+1}}}-n{\bmod {b}}^{i}}{b^{i}}}\) is the value of each digit of the number.

A natural number n is a narcissistic number if it is a fixed point of \(F_{b}\) which occurs if \(F_{b}(n)=n\).

For example, 122 in base b = 3 is a narcissistic number, because k = 3, and \(122=1^{3}+2^{3}+2^{3}\)

Sociable Narcissistic Number & Amicable Narcissistic Number

A natural number n is a sociable narcissistic number if it is a periodic point for \(F_{b}\), where \(F_{b}^{p}(n)=n\) for a positive integer p, and forms a cycle of period p. A narcissistic number is a sociable narcissistic number with \(p = 1\), and a amicable narcissistic number is a sociable narcissistic number with \(p=2\).

Reference

https://en.wikipedia.org/wiki/Narcissistic_number