Merge Sort

«  Swift Debug Assert
Resize UIImage  »

Divide And Conquer Algorithem

Many algorithm are regression: for solving one problem, it call one or more times related function to solve the small problems. These algorithm are typically follow the Divide And Conquer Method: Divide the original problem to several small related small problems. The solve these small problems regressively, and combine the result of these small problems.

Step

Divide And Conquer

  1. Divide the original problem to small problems
  2. Solve the small problems, these small problems are related to the original one but scale is small
  3. Combine the result of these small problems which will be the solution of the original problem

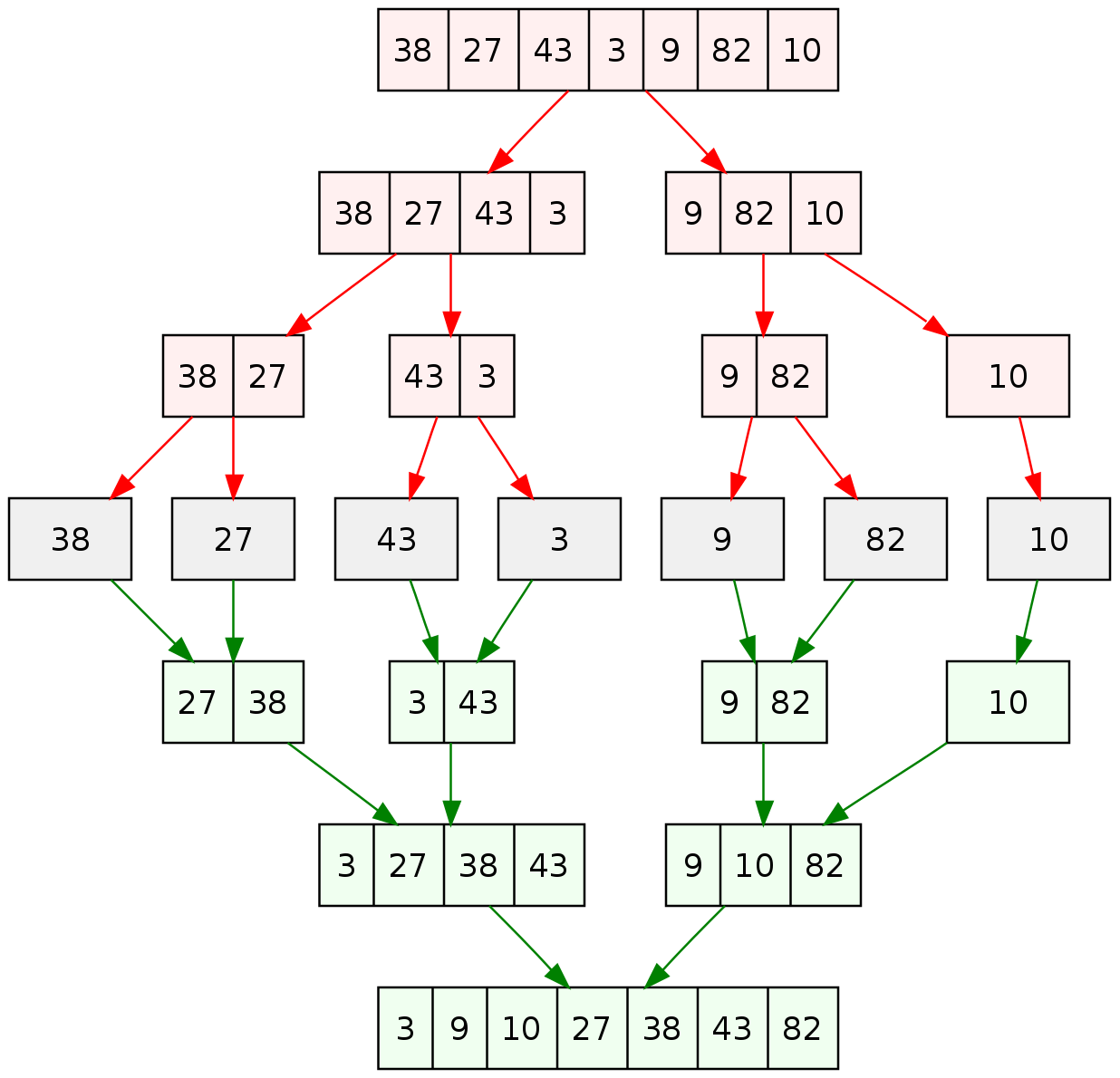
Merge Sort

  1. Divide: divide array (length: n) into 2 sub-arrays (length: n/2)
  2. Solve: use merge sort recursively sort 2 sub-arrays
  3. Combine: combine 2 sorted sub-arrays to get the final array

Example

Merge_sort_algorithm_diagram

Pseudocode

Merge(A, p, q, r) <- O(r-p+1)
n1 = q - p + 1
n2 = r - q
let L[1..n1+1] and R[1..n2+1] be new arrays
for i = 1 to n1
  L[i] = A[p + i - 1]
for j = 1 to n2
  R[j] = A[q+j]
L[n1+1] = $\infty$ <- sentry
R[n2+1] = $\infty$ <- sentry
i = 1
j = 1
for k = p to r
  if L[i] <= R[j]
    A[k] = L[i]
    i = i + 1
  else A[k] = R[j]
    j = j + 1

Merge-Sort(A, p, r)
if p < r
  q = ⌊(p+r)/2⌋
  Merge-Sort(A, p, q)
  Merge-Sort(A, q+1, r)
  Merge(A, p, q, r)

Swift Implement Merge Sort

  • Top Down
func sortArray(_ nums: [Int]) -> [Int] {
    if nums.count <= 1 { return nums }
    
    let pivot = nums.count/2
    let left = sortArray(Array(nums[0..<pivot]))
    let right = sortArray(Array(nums[pivot..<nums.count]))
    return merge(left, right)
}

// merge 2 sorted list
func merge(_ a1: [Int], _ a2: [Int]) -> [Int] {
    var i = 0
    var j = 0
    var res = [Int]()
    while i < a1.count, j < a2.count {
        if a1[i] <= a2[j] {
            res.append(a1[i])
            i += 1
        } else {
            res.append(a2[j])
            j += 1
        }
    }
    while i < a1.count {
        res.append(a1[i])
        i += 1
    }
    while j < a2.count {
        res.append(a2[j])
        j += 1
    }
    return res
}
  • Bottom Up
func sortArray(_ nums: [Int]) -> [Int] {
    if nums.count <= 1 { return nums }
    
    let n = nums.count
    
    // cache[read] for reading
    // cache[1-read] for writing
    var cache = [nums, nums]
    var read = 0 // either 0 or 1
    
    var width = 1
    while width < n {
        var i = 0
        while i < n {
            var j = i
            var l = i
            var r = i + width
            
            let lmax = min(l+width, n)
            let rmax = min(r+width, n)
            
            while l < lmax, r < rmax {
                if cache[read][l] <= cache[read][r] {
                    cache[1-read][j] = cache[read][l]
                    l += 1
                } else {
                    cache[1-read][j] = cache[read][r]
                    r += 1
                }
                j += 1
            }
            
            while l < lmax {
                cache[1-read][j] = cache[read][l]
                l += 1
                j += 1
            }
            
            while r < rmax {
                cache[1-read][j] = cache[read][r]
                r += 1
                j += 1
            }
            
            i += width * 2
        }
        
        // update width & read for new merge
        width *= 2
        read = 1 - read
    }
    
    return cache[read]
}

Time Complexity

The time complexity of Merge Sort is $O(nlog_{2}n)$.

Published on 22 Sep 2019 • Find me on Facebook, Twitter!

«  Swift Debug Assert
Resize UIImage  »

Comments

    Join the discussion for this article at here . Our comments is using Github Issues. All of posted comments will display at this page instantly.